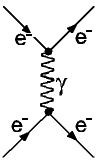Berechnung von Feynman-Diagrammen

Für einzelne Wechselwirkungen kann es viele verschiedene (unendlich) mögliche Wechselwirkungsprozesse geben. Man fragt sich, welchen Sinn das Zeichnen von Feynman-Diagrammen hat, wenn es unendlich viele Möglichkeiten zu den einzelnen Prozessen gibt, die alle zur Gesamtreaktion beitragen. Je mehr Vertices jedoch ein Feynman-Diagramm hat, desto wesentlich kleiner wird die Wahrscheinlichkeit dieses Prozesses und der Beitrag zur Gesamtreaktion.

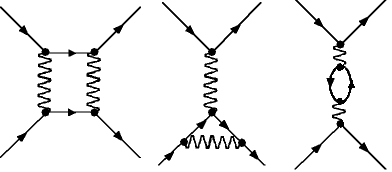
Die untenstehenden Abbildungen zeigen Beispiele für die Streuung zweier Elektronen aneinander. Der linke Prozess besitzt nur zwei Vertices, ist also wesentlich wahrscheinlicher als die rechts dargestellten Prozesse mit jeweils 4 Vertices. Die dargestellten Prozesse sind nur eine Auswahl, es gibt noch viele weitere

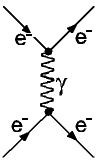
die Möller-Streuung

3 mögliche Diagramme mit gleichen äußeren Linien


Wie werden die Beiträge bzw. Wahrscheinlichkeiten der einzelnen Prozesse berechnet?

Zu jedem Vertex gehört ein Faktor 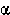alfa_Wur.gif (1009 Byte), der die Stärke der Wechselwirkung angibt. Diese sogenannte Kopplungskonstante ist zum Quadrat der zur jeweiligen Wechselwirkung gehörenden Ladungsstärke proportional. Zu jeder einzelnen der drei Wechselwirkungen gibt es also eine eigene Kopplungskonstante.
 
Elektromagnetische Wechselwirkung
Die Kopplungskonstante der elektromagnetischen Wechselwirkung wird mit aem, oftmals auch nur mit a bezeichnet (dies ist historisch bedingt, da diese Konstante zuerst entdeckt wurde). aem berechnet sich zu aem = (e²/4pe0hc) » 1/137.
Schwache Wechselwirkung
Die Kopplungskonstante der schwachen Wechselwirkung wird mit aw bezeichnet. Ihr Wert ist aw=(g2/4p) » 1/30.
Starke Wechselwirkung
Die Kopplungskonstante der schwachen Wechselwirkung wird mit as bezeichnet. Ihr Wert bei den Energien (mehr über Energieabhängigkeit in Level Level 3 Seite) der heutigen Teilchenbeschleuniger ist as=(gs2/4p) » 1/8.
Die Wahrscheinlichkeit eines Prozesses ist proportional zum Produkt aller Kopplungskonstanten 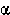der auftretenden Vertices. Der Beitrag eines Diagramms mit zwei elektromagnetischen Vertices ist also proportional zu 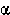2, ein Diagramm mit vier Vertices zu 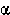4. Da mit steigender Potenz die Beiträge sehr klein werden, kann man je nach gewünschter Genauigkeit bereits bei wenigen Vertices abbrechen.
Problematisch dabei ist jedoch, dass ebenfalls die Anzahl der möglichen Diagramme mit wachsender Zahl n der vertices stark ansteigt. Während der Beitrag mit 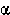hoch n abnimmt, nimmt die Anzahl der möglichen und damit beitragliefernden Diagramme mit n! zu. Bei der elektromagnetischen Wechselwirkung ist 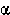klein genug, so dass dies nichts ausmacht. Bei der starken Wechselwirkung stellt dies dagegen ein echtes Problem bei den Berechnungen dar. (mehr darüber in Level Level 3 Seite)

Weiter beide Level
nächste Seite alle Level